马尔科夫链与随机过程
随机过程
定义:随机过程(stochastic process)通常是指随着时间或者空间变化的一组随机变量。随机过程是一组随机变量的集合。集合内的随机变量以时间或空间位置作为索引下标,通常是时间。根据下标是否为连续的又可以分为离散随机过程和连续随机过程。
例如,离散时间的随机过程可以写作随机变量序列的形式: \[ X_0, X_1, X_2, \cdots, X_t,\cdots \] 其中,\(X_t\)为随机变量,下标\(t\)表示时间。各个时刻的随机变量之间存在着概率关系,这是随机过程的核心。
马尔可夫性
马尔可夫随机过程(Markov process)一种特殊的随机过程。这种随机过程为随着时间进行演化的一组随机变量进行建模,并假设系统在当前时刻的状态值只与上一个状态值有关,且与更早的时刻无关,称为无记忆性(memoryless property)。
我们的目标是求得一个随机变量的联合分布概率,这样就可以依次得到各个随机变量的边际分布。而马尔可夫性质极大地简化了问题求解的计算难度。
推导
对于随机过程中的随机变量序列\(X_0, X_1, X_2, \cdots, X_T\),通常情况下各个时刻的随机变量之间存在概率关系。如果只考虑过去的信息,则当前时刻的状态\(X_t\)与过去的状态均有关系,也就是存在如下条件概率。 \[ p(X_t|X_{t-1},X_{t-2},\cdots,X_1) \] 随机过程的核心是对该条件概率建模,如果考虑过去所有时刻的状态,计算量太大。因此需要对此条件概率进行简化来降低问题求解的难度,而马尔可夫假设正是这样一种简化。
假设随机过程满足马尔可夫性,即: \[ p(X_t|X_{t-1},X_{t-2},\cdots,X_1)=p(X_t|X_{t-1}) \] 则有: \[ p(X_t|X_{t-1},X_{t-2},\cdots,X_1)=p(X_t|X_{t-1}) \] 即系统在当前时刻的状态只与上一时刻的状态有关,与更早的状态无关,这也叫做一阶马尔可夫性。利用随机向量的链式法则,可以直接求得随机变量序列联合概率的一个简洁计算公式: \[\begin{equation} p(X_0,X_1,\cdots,X_T)=p(X_0)p(X_1|X_0)p(X_2|X_1)\cdots p(X_T|X_{T-1}) \end{equation} \] 其中,\(p(X_0)\)表示初始状态的概率。(1)式表明,如果一个系统有马尔可夫性,则序列的联合概率由各个条件概率值\(p(X_t|X_{t-1})\)以及初始概率\(p(X_0)\)决定。
马尔可夫链
根据系统状态(即随机变量)是否连续,时间是否连续,可以将马尔可夫过程分为:
| 可数状态空间 | 连续状态空间 | |
|---|---|---|
| 离散时间 | 有限或可数状态空间的马尔可夫链 | 可测状态空间的马尔可夫链 |
| 连续时间 | 连续时间的马尔可夫过程 | 具有马尔可夫性的连续型随机过程 |
一般研究的是离散时间的马尔可夫链,这种随机过程的取值可以由状态转移概率\(p(X_t|X_{t-1})\)来描述条件概率。含义也就是系统上一时刻为\(X_{t-1}\)时,系统下一时刻转移到状态\(X_t\)的概率。
如果系统有\(m\)个状态,则马尔可夫链可以用一个\(m\times m\)的矩阵\(P\)来表示,其中\(P_{ij}\)表示系统从状态\(i\)转移到状态\(j\)的概率。 \[ P=\left[ \begin{matrix} p(X_0\rightarrow X_0) & p(X_0\rightarrow X_1) & \cdots & p(X_0\rightarrow X_m) \\ p(X_1\rightarrow X_0) & p(X_1\rightarrow X_1) & \cdots & p(X_1\rightarrow X_m) \\ \vdots & \vdots & \ddots & \vdots \\ p(X_m\rightarrow X_0) & p(X_m\rightarrow X_1) & \cdots & p(X_m\rightarrow X_m) \end{matrix} \right] \] \(p_{ij}\)表示由状态\(i\)转移到状态\(j\)的概率。 \[ p_{ij}=p(X_t=j|X_{t-1}=i) \] 当前时刻的状态无论处于哪一个状态,下一刻必然会转移到\(m\)中的某一个状态,即有等式约束: \[ \sum_{j=1}^{m}p_{ij}=1 \] 对于状态连续的马尔可夫链,每个时刻各个状态的值由概率密度函数来描述,状态转移概率为条件密度函数。
时齐马尔可夫性:如果任何时刻状态转移概率是相同的,则称为时齐马尔可夫链(Time-homogeneous Markov chains)。此时只有一个状态转移矩阵,在各个时刻均适用。
例子
给出某一个时刻的状态\(\mathbf{\pi}\)为一个行向量,假设状态有\(m\)个,则向量\(\mathbf{\pi}\)需要满足: \[ \sum_{i=1}^{m}\pi_i=1 \] 现在,如果令时刻\(t\)的状态为向量\(\mathbf{\pi}_t\),则可以根据前一个时刻的状态分布\(\mathbf{\pi}_{t-1}\),计算出当前时刻的状态分布\(\mathbf{\pi}_t\)。由于状态转移矩阵的第\(i\)列表示从上一个时刻的各个状态状态转移到当前时刻的状态\(i\)的概率,根据全概率公式,\(t\)时刻的状态为\(i\)的概率为: \[ \pi_{t,i}=\sum_{j=1}^{m}p_{ij}\pi_{t-1,j} \] 于是,对于所有状态,就可以写作矩阵形式为: \[ \pi_t=\mathbf{P}\pi_{t-1} \] 反复利用该公式就可以得到: \[ \pi_t=\pi_{t-1}\mathbf{P}=\pi_{t-1}\mathbf{P}\mathbf{P}=\cdots=\pi_0\mathbf{P}^t \] 因此给定初始的状态分布\(\pi_0\)和状态转移矩阵\(\mathbf{P}\),就可以计算出任意时刻的状态概率分布,这里假设是时齐的,不然每一个时刻需要使用不同的状态转移矩阵。
进一步的,我们可以定义n步转移概率为从状态\(i\)经过\(n\)转移到状态\(j\)的概率。记为: \[ p_{ij}^n=p(X_n=j|X_{0}=i) \] 以及n步时齐的马尔科夫链的转移矩阵为: \[ P^n=\left[ \begin{matrix} p_{11}^{(n)} & p_{12}^{(n)} & \cdots & p_{1m}^{(n)} \\ p_{21}^{(n)} & p_{22}^{(n)} & \cdots & p_{2m}^{(n)} \\ \vdots & \vdots & \ddots & \vdots \\ p_{m1}^{(n)} & p_{m2}^{(n)} & \cdots & p_{mm}^{(n)} \end{matrix} \right] \] 特殊的,如果\(n=1\),则就是状态转移矩阵。
根据定义,\(n\)步转移概率满足\(Chapman-Kolmogorov equations\)(简称CK方程): \[ p_{ij}^{(n)}=\sum_{k=1}^{m}p_{ik}^{(l)}p_{kj}^{(n-l)} \] 即从状态\(i\)经过\(n\)次转移进入状态\(j\)的概率,等于从状态\(i\)先经过\(l\)步转移到状态\(k\),再乘以经过\((n-l)\)步转移到状态\(j\)的概率,并对所有的\(k\)求和。
根据\(C-K\)方程,对于\(n\)步的转移矩阵,有如下的乘积关系: \[ \mathbf{P}^{n+l}=\mathbf{P}^{(n)}\mathbf{P}^{(l)} \] 由此我们得到\(\mathbf{P}^n=\mathbf{P}^{(n)}\)
马尔可夫链状态的性质
实际上,并非每个状态经过转移后都可能会转移到另一个状态,因此我们说如果可以从状态\(i\)转移到\(j\),即存在\(n \geq 0\)使得 \[ p_{ij}^{(n)}\gt 0 \] 则称状态\(i\)到状态\(j\)是可达的,记作\(i \rightarrow j\). 如果\(i \rightarrow j\)且\(j \rightarrow i\),则称这两个状态是互通的,记为\(i \leftrightarrow j\)。
互通具有自反性,对称性,传递性。因此,互通是第一种等价关系。所有互通的状态属于同一个等价类,可以按照互通性将所有状态划分分成若干个不相交的子集。
根据可约关系,如果一个马尔可夫链任意两个都是互通的,则称它是不可约的(irreducible),否则是可约的。
周期
状态\(i\)的周期\(d(i)\)定义为该状态出发,经过n步之后回到该状态,这些n的最大公约数。 \[ d(i) = gcd\{n>0:p_{ii}^{(n)}>0\}\] 其中gcd为最大公约数。如果对所有\(n \gt 0\)都有\(p_{ii}^{(n)}\gt 0\),则称周期为无穷大\((+\infty)\)。如果状态的周期\(d(i)\gt>1\),则称该状态是周期的。如果状态的周期为1,则它为非周期的。
- 如果两个状态互通,则它们的周期相同。
推论
1. 如果不可约的马尔可夫链有周期性状\(i\),则其所有状态为周期性状态 2.
对于不可约的马尔可夫链,如果一个状态\(i\)是非周期的,则所有的状态都是非周期的。
令\(f_{ij}\)表示从状态\(i\)出发迟早将转移状态\(j\)的概率。如果\(i \ne j\),当且仅当从\(i\)到\(j\)可达时\(f_{ij}\)为正。\(f_{ii}\)表示从状态\(i\)出发迟早会返回该状态的概率。如果\(f_{ii}=1\),则称状态\(i\)是常返的,否则是非常返的。
推论 - 如果\(i\)是常返的,且\(i \leftrightarrow j\),则j是常返的。
- 如果\(i\leftrightarrow j\),且j是常返的,则\(f_{ij}=1\)。
平稳分布与极限分布
对于式子 \[
\pi_t=\pi_{t-1}\mathbf{P}=\pi_{t-1}\mathbf{P}\mathbf{P}=\cdots=\pi_0\mathbf{P}^t
\]
可以发现一个有趣的性质,对于任意的初始状态分布,随着状态转移的进行,最后系统状态的概率分布趋向于一个稳定的值。
平稳分布:假设状态空间的大小为m,向量\(\pi\)为状态的概率分布。对状态转移矩阵\(\mathbf{P}\)的马尔可夫链,如果存在一个概率分布\(\pi\)满足 \[
\pi \mathbf{P} = \pi
\] 则称此分布\(\pi\)为平稳分布。其意义为如果当前时刻的状态如果服从此分布,转移到下一时刻之后还服从此分布,因此称为“平稳”。
平稳分布即为状态转移矩阵的转置矩阵\(\mathbf{P}^T\)归一化的特征向量,且特征值为1。 (其实就是为了符合特征向量左乘的定义) \[ (\pi \mathbf{P})^T = \mathbf{P}^T\pi^T = \pi^T \]
那么,给定一个状态转移矩阵\(\mathbf{P}\),就可以通过求解特征方程来得到对应的平稳分布
⚠️注意:并非所有的马尔可夫链都存在平稳分布且唯一。
马尔可夫性质的应用
细致平稳条件
某些应用需要在给定状态概率分布\(\pi\)的条件下构造出一个马尔可夫链,即构造出一个状态转移矩阵\(\mathbf{P}\),使其平稳分布是\(\pi\)。细致平稳条件就是解决此问题的一种办法。 \[\begin{equation} \pi_{i}p_{ij} = \pi_j p_{ji} \end{equation} \]
即对于\(\forall i,j\),处于状态\(i\)的概率乘以从状态\(i\)转移到状态\(j\)的概率等于处于状态\(j\)的概率乘以从状态\(j\)转移到状态\(i\)到概率,则\(\pi\)为马尔可夫链的平稳分布。
式子(2)称为细致平稳条件。
!注意, \(\mathbf{P}\)和\(\pi\)满足细致平衡条件是\(\pi\)为\(\mathbf{P}\)的平稳分布的充分条件而非必要条件。
直观上来说,平稳分布意味着对于任意一个状态,从所有状态转入到该状态的概率值与从状态的概率值相等(即从该状态转出去的概率值)。而细致平衡条件显然是一个更严格的要求,要求对任意的两个状态i与j,从i转入到j到概率和从j转入到i的概率相等。隐式马尔可夫模型
在一些实际应用中并不能直接观察得到系统的状态值,状态的值是隐含的,只能得到一组称为观测的值。隐式马尔可夫模型就是描述了观测变量与状态变量之间的概率关系。
定义观测序列:
\[
\mathbf{x}={x_1,\cdots,x_T}
\]
它是能够直接观察或者计算得到的值,是一个随机变量序列。任何一时刻的观测值都来自有限的观测集
\[
V = {v_1,\cdots,v_m}
\] 定义状态序列 \[
\mathbf{z}={z_1,\cdots,z_T}
\]
状态序列也是一个随机变量序列。任意时刻的状态值也来自有限的状态集 \[
S={s_1,\cdots,s_n}
\]
状态序列是一个马尔可夫链,其状态转移矩阵为\(\mathbf{A}\)。状态随着时间演化,每个时刻的状态值决定了观测值。
例子:
假如要识别一个视频里的人的各种动作,那么状态即为要识别的动作,例如站立、坐下和行走等,在进行识别之前无法得知其值。观测是能够直接得到的值,如人体身上各个关键点点坐标,隐式马尔可夫模型通过观测值来推断状态值,从而识别出动作。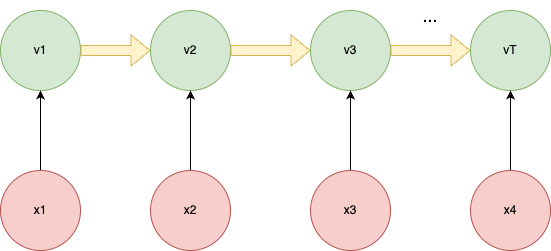
除了状态转移矩阵外,隐式马尔可夫模型还有观测矩阵\(\mathbf{B}\),其元素为: \[ b_{ij}=p(x_t=v_j|z_t=s_i) \] 该值表示t时刻状态值为\(s_i\)时观测值为\(v_j\)的概率。观测矩阵的第i行是状态为\(s_i\)时观测值为各个值的概率分布。那么,假设初始状态分布的概率分布为\(\pi\),隐马尔可夫模型可以表示为五元组: \[ \{S,V,\pi,\mathbf{A},\mathbf{B}\} \] 实际应用中,一般假设状态转移矩阵\(\mathbf{A}\)和观测矩阵\(\mathbf{B}\)在任何时刻都是相同的,即与时间无关,马尔可夫是时齐的,从而简化问题的计算难度
作为一个例子:
假设我们无法得知天气的情况,但能得知一个人在各种天气下的活动情况,{睡觉、跑步、逛街},那么天气在这个问题中就是状态值,而活动就是观测值。在隐马尔可夫模型中,状态和观测是根据实际问题人工设定的;状态转移矩阵和观测矩阵通过样本学习得到。在给定观测序列\(\mathbf{x}\)的条件下,可以通过计算出状态序列\(\mathbf{z}\)出现的概率即条件概率\(p(\mathbf{z}|\mathbf{x})\)。
观测序列的产生过程为:系统在1时刻处于状态\(z_1\),在该状态下得到观测值为\(x_1\)。接下来从\(z_1\)转移到\(z_2\),并在此状态下得到观测值\(x_2\)。以此类推,得到整个观测序列。由于每一时刻的观测值只依赖于本时刻的状态值,因此当出现状态序列\(\mathbf{z}\)的时候观测序列为\(\mathbf{x}\)的概率为: \[ \begin{align} p(\mathbf{z},\mathbf{x}) &= p(\mathbf{z})p(\mathbf{z}|\mathbf{x}) \\ &= p(z_{T}|z_{T-1})p(z_{T-1}|z_{T-2})\cdots p(z_{1}|z_{0}) \\ &\quad \times p(x_{T}|z_{T})p(x_{T-1}|z_{T-1})\cdots p(x_{1}|z_{1})\\ &= (\prod_{t=1}^{T} a_{z_{t-1}z_t}) \times \prod_{t=1}^{T} b_{z_t x_t} \\ \end{align} \] 其中,约定\(p(z_1|z_0)=p(z_1)\)为状态的初始概率。