集合通信

集合通信

集合通信是分布式训练中非常重要的一个概念，它是指在分布式系统中，多个计算设备之间进行通信的一种方式。

通信模型

假定在一个分布式机器学习集群中，存在p个计算设备，并由一个网络来连接所有的设备。每个设备有自己的独立内存，并且所有设备间的通信都通过该网络传输。同时，每个设备都有一个编号i，其中i的范围从1到p。 设备之间的点对点（Point-to-Point, P2P）通信由全双工传输(Full-Duplex Transmission)实现。该通信模型的基本行为可以定义如下：

  • 每次通信有且仅有一个发送者（Sender）和一个接收者（Receiver）。在某个特定时刻，每个设备仅能至多发送或接收一个消息（Message）。每个设备可以同时发送一个消息和接收一个消息。一个网络中可以同时传输多个来自于不同设备的消息。
  • 传输一个长度为l个字节（Byte）的消息会花费a + b × l的时间，其中a代表延迟（Latency），即一个字节通过网络从一个设备出发到达另一个设备所需的时间；b代表传输延迟（Transmission Delay），即传输一个具有l个字节的消息所需的全部时间。前者取决于两个设备间的物理距离（如跨设备、跨机器、跨集群等），后者取决于通信网络的带宽。需要注意的是，这里简化了传输延迟的定义，其并不考虑在真实网络传输中会出现的丢失的消息（Dropped Message）和损坏的消息（Corrupted Message）的情况。

我们可以定义集合通信算子(即通信的行为)，并且分析算子的通信性能。

Broadcast

一个分布式机器学习系统经常需要将一个设备上的模型参数或者配置文件广播（Broadcast）给其余全部设备。因此，可以把Broadcast算子定义为从编号为i的设备发送长度为l字节的消息给剩余的个设备。

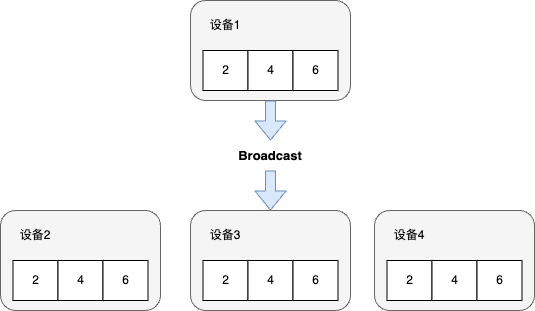
broadcast

一种简单实现Broadcast的算法是在设备上实现一个循环，该循环使用p − 1次Send/Receive操作来将数据传输给相应设备。然而，该算法不能达到并行通信的目的（该算法只有(a + b × l) × (p − 1)的线性时间复杂度）。

为此，可以利用分治思想对上述简单实现的Broadcast算法进行优化。假设所有的设备可以重新对编号进行排列，使得Broadcast的发送者为编号为1的设备。同时，为了简化计算过程，假设对某个自然数n，p = 2n。 现在，可以通过从1向p/2发送一次信息把问题转换为两个大小为的子问题：

  1. 编号为1的设备对编号1到编号p/2 − 1的Broadcast
  2. 以及编号为p/2的设备对编号p/2到编号p的Broadcast。

接下来就可以通过在这两个子问题上进行递归来完成这个算法，并把临界条件定义为编号为i的设备在[i, i]这个区间中的Broadcast。此时，由于本身已经拥有该信息，不需要做任何操作便可直接完成Broadcast。这个优化后的算法为(a + b × l) × logp时间复杂度，因为在算法的每一阶段（编号为t），有2t个设备在并行运行Broadcast算子。同时，算法一定会在logp步之内结束。

Reduce

在分布式机器学习系统中，另一个常见的操作是将不同设备上的计算结果进行聚合（Aggregation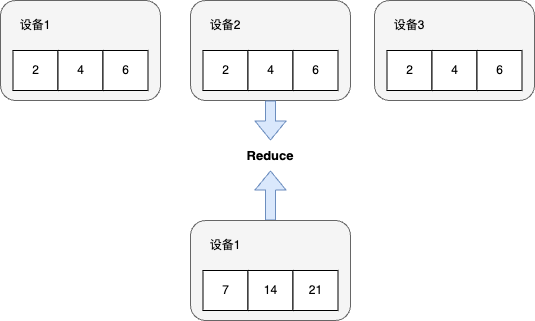）。 Reduce 例如，将每个设备计算的本地梯度进行聚合，计算梯度之和（Summation）。这些聚合函数（表达为f）往往符合结合律（Associative Law）和交换律（Commutative Law）。这些函数由全部设备共同发起，最终聚合结果存在编号为i的设备上。常见聚合函数有加和、乘积、最大值和最小值。集合通信将这些函数表达为Reduce算子。

一个简易的Reduce的优化实现同样可以用分治思想来实现，即把1到p/2 − 1的Reduce结果存到编号为1的设备中，然后把p/2到p的Reduce结果存到p/2上。最后，可以把p/2的结果发送至1，执行f，并把最后的结果存至i。假设f的运行时间复杂度为常数并且其输出信息的长度l不改变，Reduce的时间复杂度仍然为(a + b × l) × logp。

AllReduce

集合通信通过引入AllReduce算子，从而将Reduce函数f的结果存至所有设备上。 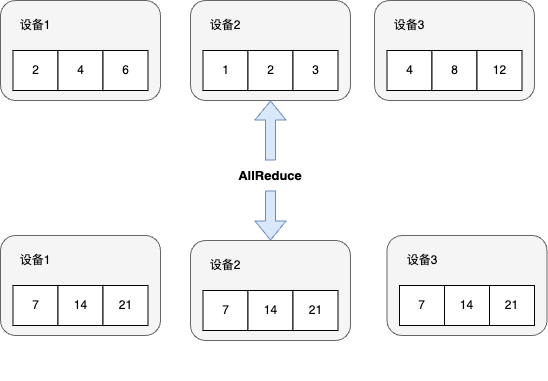AllReduce

一种简单的AllReduce实现方法是首先调用Reduce算法并将聚合结果存到编号为1的设备上。然后，再调用Broadcast算子将聚合结果广播到所有的设备。这种简单的AllReduce实现的时间复杂度为(a + b × l) × logp。

Gather

Gather算子可以将全部设备的数据全部收集（Gather）到编号为i的设备上。 Gather 在收集函数（Gather Function）符合结合律和交换律的情况下，可以通过将其设为Reduce算子中的f来实现Gather算子。但是，在这种情况下，无论是基于链表还是数组的实现，在每一步的Reduce操作中f的时间复杂度和输出长度l都发生了改变。因此，Gather的时间复杂度是a × logp + (p − 1) × b × l。这是因为在算法的每一阶段t，传输的信息长度为2t × l。

AllGather

AllGather算子会把收集的结果分发到全部的设备上。 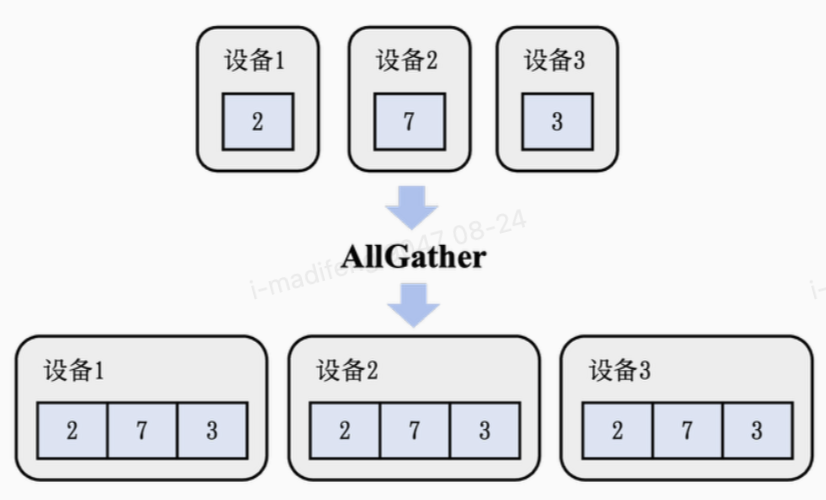allgather 在这里，一个简单的方法是使用Gather和Broadcast算子把聚合结果先存到编号为1的设备中，再将其广播到剩余的设备上。这会产生一个的时间复杂度a × logp + (p − 1) × b × l(a + p × b × l) × logp，因为在广播时，如果忽略链表/数组实现所带来的额外空间开销，每次通信的长度为pl而不是l。简化后，得到了一个 a × logp + p × l × b × logp的时间复杂度。在一个基于超立方体的算法下，可以将其进一步优化到和Gather算子一样的时间复杂度a × logp + (p − 1) × b × l。

Scatter

Scatter算子可以被视作Gather算子的逆运算：把一个存在于编号为i的设备上，长度为p（信息长度为p × l）的链式数据结构中的值分散到每个设备上，使得编号为i的设备会得到L[i]的结果。 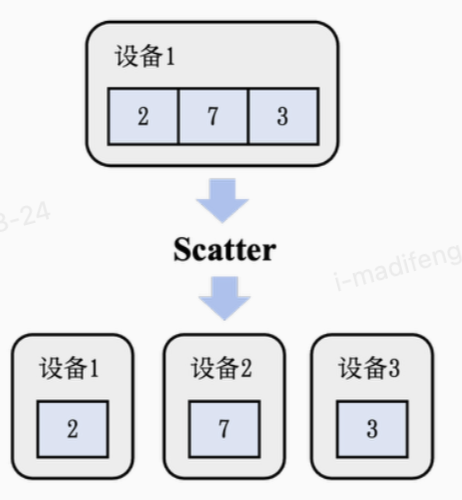scatter 可以通过模仿Gather算法设计一个简易的Scatter实现：每一步的运算中，我们把现在的子链继续对半切分，并把前半段和后半段作为子问题进行递归。这时候，在算法的每一阶段t，传输的信息长度为l × 2m − t，其中是算法总共运行的步骤，不会超过 （见Broadcast算子的介绍）。最终，Scatter算子的简易实现和Gather算子一样都有a × logp + (p − 1) × b × l 的时间复杂度。在机器学习系统中，Scatter算子经常同时被用于链式数据结构和可切分的数据结构，例如张量在一个维度上的p等分等。