随机过程

定义：随机过程（stochastic process）通常是指随着时间或者空间变化的一组随机变量。随机过程是一组随机变量的集合。集合内的随机变量以时间或空间位置作为索引下标，通常是时间。根据下标是否为连续的又可以分为离散随机过程和连续随机过程。

例如，离散时间的随机过程可以写作随机变量序列的形式：

X₀, X₁, X₂, ⋯, X_t, ⋯

其中，X_t为随机变量，下标t表示时间。各个时刻的随机变量之间存在着概率关系，这是随机过程的核心。

马尔可夫性

马尔可夫随机过程（Markov process）一种特殊的随机过程。这种随机过程为随着时间进行演化的一组随机变量进行建模，并假设系统在当前时刻的状态值只与上一个状态值有关，且与更早的时刻无关，称为无记忆性(memoryless property)。

我们的目标是求得一个随机变量的联合分布概率，这样就可以依次得到各个随机变量的边际分布。而马尔可夫性质极大地简化了问题求解的计算难度。

推导

对于随机过程中的随机变量序列X₀, X₁, X₂, ⋯, X_T，通常情况下各个时刻的随机变量之间存在概率关系。如果只考虑过去的信息，则当前时刻的状态X_t与过去的状态均有关系，也就是存在如下条件概率。

p(X_t|X_t − 1, X_t − 2, ⋯, X₁)

随机过程的核心是对该条件概率建模，如果考虑过去所有时刻的状态，计算量太大。因此需要对此条件概率进行简化来降低问题求解的难度，而马尔可夫假设正是这样一种简化。

假设随机过程满足马尔可夫性，即：

p(X_t|X_t − 1, X_t − 2, ⋯, X₁) = p(X_t|X_t − 1)

则有：

p(X_t|X_t − 1, X_t − 2, ⋯, X₁) = p(X_t|X_t − 1)

即系统在当前时刻的状态只与上一时刻的状态有关，与更早的状态无关，这也叫做一阶马尔可夫性。利用随机向量的链式法则，可以直接求得随机变量序列联合概率的一个简洁计算公式:

p(X₀, X₁, ⋯, X_T) = p(X₀)p(X₁|X₀)p(X₂|X₁)⋯p(X_T|X_T − 1)

其中，p(X₀)表示初始状态的概率。(1)式表明，如果一个系统有马尔可夫性，则序列的联合概率由各个条件概率值p(X_t|X_t − 1)以及初始概率p(X₀)决定。

马尔可夫链

根据系统状态(即随机变量)是否连续，时间是否连续，可以将马尔可夫过程分为：

	可数状态空间	连续状态空间
离散时间	有限或可数状态空间的马尔可夫链	可测状态空间的马尔可夫链
连续时间	连续时间的马尔可夫过程	具有马尔可夫性的连续型随机过程

一般研究的是离散时间的马尔可夫链，这种随机过程的取值可以由状态转移概率p(X_t|X_t − 1)来描述条件概率。含义也就是系统上一时刻为X_t − 1时，系统下一时刻转移到状态X_t的概率。

如果系统有m个状态，则马尔可夫链可以用一个m × m的矩阵P来表示，其中P_ij表示系统从状态i转移到状态j的概率。

$$ P=\left[ \begin{matrix} p(X_0\rightarrow X_0) & p(X_0\rightarrow X_1) & \cdots & p(X_0\rightarrow X_m) \\ p(X_1\rightarrow X_0) & p(X_1\rightarrow X_1) & \cdots & p(X_1\rightarrow X_m) \\ \vdots & \vdots & \ddots & \vdots \\ p(X_m\rightarrow X_0) & p(X_m\rightarrow X_1) & \cdots & p(X_m\rightarrow X_m) \end{matrix} \right] $$

p_ij表示由状态i转移到状态j的概率。

p_ij = p(X_t = j|X_t − 1 = i)

当前时刻的状态无论处于哪一个状态，下一刻必然会转移到m中的某一个状态，即有等式约束：

$$ \sum_{j=1}^{m}p_{ij}=1 $$

对于状态连续的马尔可夫链，每个时刻各个状态的值由概率密度函数来描述，状态转移概率为条件密度函数。

时齐马尔可夫性：如果任何时刻状态转移概率是相同的，则称为时齐马尔可夫链(Time-homogeneous Markov chains)。此时只有一个状态转移矩阵，在各个时刻均适用。

例子

给出某一个时刻的状态π为一个行向量，假设状态有m个，则向量π需要满足：

$$ \sum_{i=1}^{m}\pi_i=1 $$

现在，如果令时刻t的状态为向量π_t，则可以根据前一个时刻的状态分布π_t − 1，计算出当前时刻的状态分布π_t。由于状态转移矩阵的第i列表示从上一个时刻的各个状态状态转移到当前时刻的状态i的概率，根据全概率公式，t时刻的状态为i的概率为：

$$ \pi_{t,i}=\sum_{j=1}^{m}p_{ij}\pi_{t-1,j} $$

于是，对于所有状态，就可以写作矩阵形式为：

π_t = Pπ_t − 1

反复利用该公式就可以得到:

π_t = π_t − 1P = π_t − 1PP = ⋯ = π₀P^t

因此给定初始的状态分布π₀和状态转移矩阵P，就可以计算出任意时刻的状态概率分布，这里假设是时齐的，不然每一个时刻需要使用不同的状态转移矩阵。

进一步的，我们可以定义n步转移概率为从状态i经过n转移到状态j的概率。记为：

p_ijⁿ = p(X_n = j|X₀ = i)

以及n步时齐的马尔科夫链的转移矩阵为：

$$ P^n=\left[ \begin{matrix} p_{11}^{(n)} & p_{12}^{(n)} & \cdots & p_{1m}^{(n)} \\ p_{21}^{(n)} & p_{22}^{(n)} & \cdots & p_{2m}^{(n)} \\ \vdots & \vdots & \ddots & \vdots \\ p_{m1}^{(n)} & p_{m2}^{(n)} & \cdots & p_{mm}^{(n)} \end{matrix} \right] $$

特殊的，如果n = 1，则就是状态转移矩阵。

根据定义，n步转移概率满足Chapman − Kolmogorovequations(简称CK方程)：

$$ p_{ij}^{(n)}=\sum_{k=1}^{m}p_{ik}^{(l)}p_{kj}^{(n-l)} $$

即从状态i经过n次转移进入状态j的概率，等于从状态i先经过l步转移到状态k，再乘以经过(n − l)步转移到状态j的概率，并对所有的k求和。

根据C − K方程，对于n步的转移矩阵，有如下的乘积关系：

P^n + l = P⁽ⁿ⁾P^(l)

由此我们得到Pⁿ = P⁽ⁿ⁾

马尔可夫链状态的性质

实际上，并非每个状态经过转移后都可能会转移到另一个状态，因此我们说如果可以从状态i转移到j,即存在n ≥ 0使得

p_ij⁽ⁿ⁾ > 0

则称状态i到状态j是可达的，记作i → j. 如果i → j且j → i，则称这两个状态是互通的，记为i ↔︎ j。

互通具有自反性，对称性，传递性。因此，互通是第一种等价关系。所有互通的状态属于同一个等价类，可以按照互通性将所有状态划分分成若干个不相交的子集。

根据可约关系，如果一个马尔可夫链任意两个都是互通的，则称它是不可约的（irreducible），否则是可约的。

周期

状态i的周期d(i)定义为该状态出发，经过n步之后回到该状态，这些n的最大公约数。

d(i) = gcd{n > 0 : p_ii⁽ⁿ⁾ > 0}

其中gcd为最大公约数。如果对所有n > 0都有p_ii⁽ⁿ⁾ > 0，则称周期为无穷大(+∞)。如果状态的周期d(i) >  > 1,则称该状态是周期的。如果状态的周期为1，则它为非周期的。

• 如果两个状态互通，则它们的周期相同。

推论

1. 如果不可约的马尔可夫链有周期性状i，则其所有状态为周期性状态
2. 对于不可约的马尔可夫链，如果一个状态i是非周期的，则所有的状态都是非周期的。

令f_ij表示从状态i出发迟早将转移状态j的概率。如果i ≠ j，当且仅当从i到j可达时f_ij为正。f_ii表示从状态i出发迟早会返回该状态的概率。如果f_ii = 1,则称状态i是常返的，否则是非常返的。

推论

• 如果i是常返的，且i ↔︎ j，则j是常返的。
• 如果i ↔︎ j，且j是常返的，则f_ij = 1。

平稳分布与极限分布

对于式子

π_t = π_t − 1P = π_t − 1PP = ⋯ = π₀P^t

可以发现一个有趣的性质，对于任意的初始状态分布，随着状态转移的进行，最后系统状态的概率分布趋向于一个稳定的值。 平稳分布：假设状态空间的大小为m，向量π为状态的概率分布。对状态转移矩阵P的马尔可夫链，如果存在一个概率分布π满足

πP = π

则称此分布π为平稳分布。其意义为如果当前时刻的状态如果服从此分布，转移到下一时刻之后还服从此分布，因此称为“平稳”。

平稳分布即为状态转移矩阵的转置矩阵P^T归一化的特征向量，且特征值为1。 （其实就是为了符合特征向量左乘的定义）

(πP)^T = P^Tπ^T = π^T

那么，给定一个状态转移矩阵P，就可以通过求解特征方程来得到对应的平稳分布

⚠️注意：并非所有的马尔可夫链都存在平稳分布且唯一。

马尔可夫性质的应用

细致平稳条件

某些应用需要在给定状态概率分布π的条件下构造出一个马尔可夫链，即构造出一个状态转移矩阵P，使其平稳分布是π。细致平稳条件就是解决此问题的一种办法。

π_ip_ij = π_jp_ji

即对于∀i, j,处于状态i的概率乘以从状态i转移到状态j的概率等于处于状态j的概率乘以从状态j转移到状态i到概率，则π为马尔可夫链的平稳分布。

式子(2)称为细致平稳条件。

！注意， P和π满足细致平衡条件是π为P的平稳分布的充分条件而非必要条件。

直观上来说，平稳分布意味着对于任意一个状态，从所有状态转入到该状态的概率值与从状态的概率值相等（即从该状态转出去的概率值）。而细致平衡条件显然是一个更严格的要求，要求对任意的两个状态i与j，从i转入到j到概率和从j转入到i的概率相等。

隐式马尔可夫模型

在一些实际应用中并不能直接观察得到系统的状态值，状态的值是隐含的，只能得到一组称为观测的值。隐式马尔可夫模型就是描述了观测变量与状态变量之间的概率关系。

定义观测序列：

x = x₁, ⋯, x_T

它是能够直接观察或者计算得到的值，是一个随机变量序列。任何一时刻的观测值都来自有限的观测集

V = v₁, ⋯, v_m

定义状态序列

z = z₁, ⋯, z_T

状态序列也是一个随机变量序列。任意时刻的状态值也来自有限的状态集

S = s₁, ⋯, s_n

状态序列是一个马尔可夫链，其状态转移矩阵为A。状态随着时间演化，每个时刻的状态值决定了观测值。

例子：

假如要识别一个视频里的人的各种动作，那么状态即为要识别的动作，例如站立、坐下和行走等，在进行识别之前无法得知其值。观测是能够直接得到的值，如人体身上各个关键点点坐标，隐式马尔可夫模型通过观测值来推断状态值，从而识别出动作。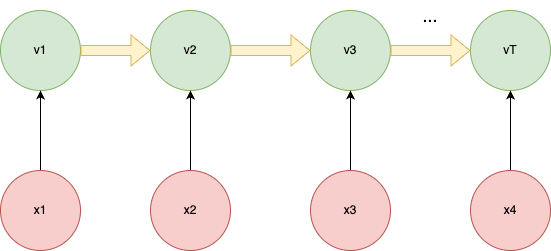

hmm

除了状态转移矩阵外，隐式马尔可夫模型还有观测矩阵B，其元素为：

b_ij = p(x_t = v_j|z_t = s_i)

该值表示t时刻状态值为s_i时观测值为v_j的概率。观测矩阵的第i行是状态为s_i时观测值为各个值的概率分布。那么，假设初始状态分布的概率分布为π，隐马尔可夫模型可以表示为五元组：

{S, V, π, A, B}

实际应用中，一般假设状态转移矩阵A和观测矩阵B在任何时刻都是相同的，即与时间无关，马尔可夫是时齐的，从而简化问题的计算难度

作为一个例子：

假设我们无法得知天气的情况，但能得知一个人在各种天气下的活动情况，{睡觉、跑步、逛街}，那么天气在这个问题中就是状态值，而活动就是观测值。

在隐马尔可夫模型中，状态和观测是根据实际问题人工设定的；状态转移矩阵和观测矩阵通过样本学习得到。在给定观测序列x的条件下，可以通过计算出状态序列z出现的概率即条件概率p(z|x)。

观测序列的产生过程为：系统在1时刻处于状态z₁，在该状态下得到观测值为x₁。接下来从z₁转移到z₂，并在此状态下得到观测值x₂。以此类推，得到整个观测序列。由于每一时刻的观测值只依赖于本时刻的状态值，因此当出现状态序列z的时候观测序列为x的概率为：

$$ \begin{align} p(\mathbf{z},\mathbf{x}) &= p(\mathbf{z})p(\mathbf{z}|\mathbf{x}) \\ &= p(z_{T}|z_{T-1})p(z_{T-1}|z_{T-2})\cdots p(z_{1}|z_{0}) \\ &\quad \times p(x_{T}|z_{T})p(x_{T-1}|z_{T-1})\cdots p(x_{1}|z_{1})\\ &= (\prod_{t=1}^{T} a_{z_{t-1}z_t}) \times \prod_{t=1}^{T} b_{z_t x_t} \\ \end{align} $$

其中，约定p(z₁|z₀) = p(z₁)为状态的初始概率。