强化学习——马尔可夫决策过程
马尔可夫决策过程
强化学习的基础算法之一就是马尔可夫决策过程(Markov Decision Process, MDP),是一个用于在结果部分随机、部分由决策者控制的场景下建模决策的数学框架。它由状态集、动作集、状态转移概率、奖励函数和折扣因子组成,是强化学习(RL)中的基础概念,用于在机器人学、自动化、经济学等领域解决序贯决策问题。 其核心思想是,智能体的下一步状态仅取决于当前状态和所采取的动作,满足马尔可夫性质,目标是找到一个策略来最大化累积奖励
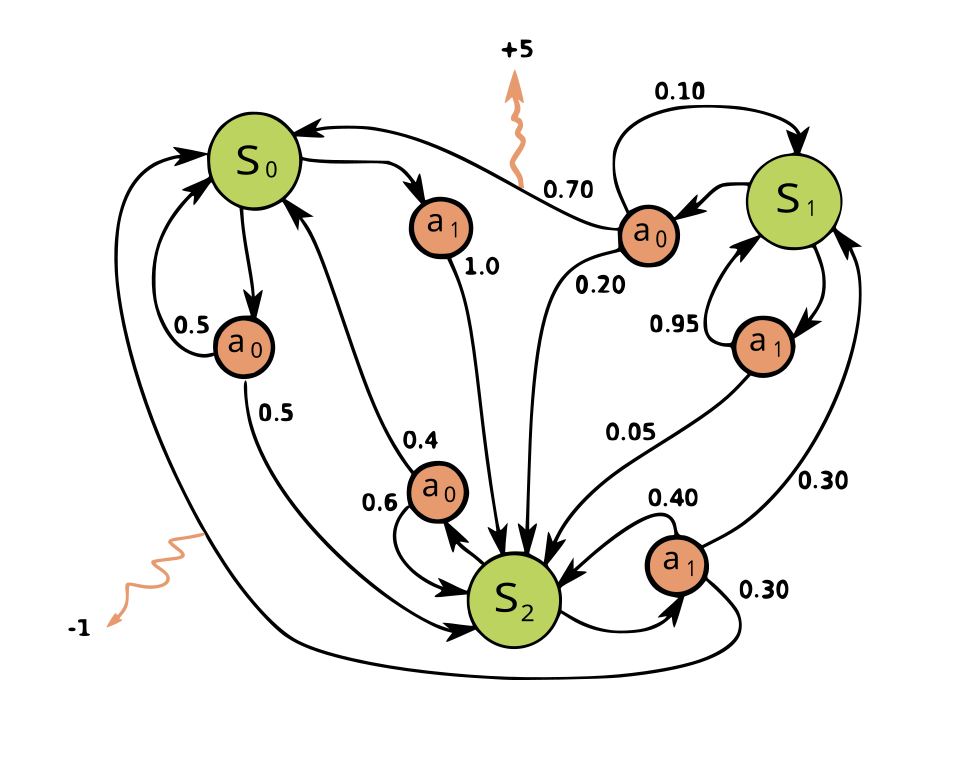
背景知识
概率论的研究对象是静态的随机现象,而随机过程的研究对象是随时间演变的随机现象(例如天气随时间的变化、城市交通随时间的变化)。在随机过程中,随机现象在某时刻的取值是一个向量随机变量,用St表示,所有可能的状态组成状态集合S。随机现象便是状态的变化过程。在某时刻t的状态St通常取决于t时刻之前的状态。
MDP的核心在于马尔可夫性质:系统的下一个状态仅取决于当前状态和当前采取的动作,而与之前的状态或历史决策无关。这意味着当前状态提供了做出最优决策所需的所有信息。状态和行动空间可能是有限的,也可能是无限的。一些具有可数无限状态和行动空间的过程可以简化为具有有限状态和行动空间的过程。
马尔可夫奖励过程
在马尔可夫过程的基础上加入奖励函数R和衰减因子γ就成为了一个马尔可夫奖励过程(Markov reward process, MRP),一个标准的马尔可夫奖励过程由五个关键元素组成,通常表示为一个五元组 (S, A, P, R, γ):
- 状态空间 (S):所有可能环境状态的集合。在迷宫游戏中,这可以是智能体所在的具体坐标位置。
- 动作空间 (A):智能体在每个状态下可以采取的所有可能动作的集合。例如,在迷宫中可能是“向前”、“向后”、“向左”、“向右”。
- 状态转移概率 (P):定义了在给定当前状态 (s) 和采取动作 (a) 时,转移到下一个状态 (s′) 的概率,即 (P(s′|s, a))。
- 奖励函数 (R):定义了智能体从环境中获得的即时奖励。通常表示为 (R(s, a, s′)),即从状态 (s) 采取动作 (a) 转移到状态 (s′) 所获得的奖励值。
- 折扣因子 (γ):一个介于 0 到 1 之间的值,用于衡量未来奖励相对于当前奖励的重要性。引入折扣因子的理由为远期利益具有一定不确定性,有时我们更希望能够尽快获得一些奖励,所以我们需要对远期利益打一些折扣。γ接近 1 的更关注长期的累计奖励,γ接近 0 的更考虑短期奖励。
回报
在马尔可夫奖励过程中,从t时刻某一状态St开始直到终止状态时,所有奖励的衰减之和称为回报。回报Gt定义为:
$$ G_t = R_{t} + \gamma R_{t+1} + \gamma^2 R_{t+2} + \cdots = \sum_{k=0}^{\infty} \gamma^k R_{t+k} $$
其中,Rt是在t时刻获得的奖励,γ是衰减因子,用于衡量未来奖励相对于当前奖励的重要性。
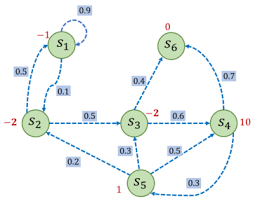
在这个例子里直接给出了每个状态获得的奖励。
价值函数
在马尔可夫奖励过程中,一个状态的期望回报(即从这个状态出发的未来累积奖励的期望)被称为这个状态的价值(value)。所有状态的价值就组成了价值函数(value function),价值函数的输入为某个状态,输出为这个状态的价值。我们将价值函数写成
$$\begin{align*} V(s) = \mathbb{E}[G_t|S_t=s] \end{align*} $$
某个状态的价值 V,等于从这个状态出发,未来所有可能路径的回报总和(G)的平均值(期望 𝔼)。其可以展开为:
$$ \begin{align*} \mathbb{E}[G_t|S_t=s] &= \mathbb{E}[R_{t} + \gamma R_{t+1} + \gamma^2 R_{t+2} + \cdots |S_t=s] \\ &= \mathbb{E}[R_{t}+\gamma (R_{t+1} + \gamma R_{t+2} + \cdots) |S_t=s] \\ &= \mathbb{E}[R_{t}+\gamma G_{t+1}|S_t=s] \\ \end{align*} $$
如果我们站在下一时刻 t + 1 的状态 St + 1 上,根据同样的定义,就有:
$$\begin{align*} V(S_{t+1}) = \mathbb{E}[G_{t+1} | S_{t+1}] \end{align*} $$
即:下一状态的价值 = 下一状态未来回报的期望。在推导的最后一行,我们有项 γGt + 1。在求期望 𝔼 的时候,我们可以把 Gt + 1 替换成它的“平均表现”,也就是 V(St + 1)。这是因为我们在 St,不知道下一步 St + 1 会去哪个状态,但是我们知道,无论 St + 1 具体是哪个状态,那个状态对应的未来期望回报就是 V(St + 1)。所以,我们只需要对 St + 1 的分布求期望即可。
于是我们得到:
$$ \begin{align*} V(s) &= \mathbb{E}[R_{t}+\gamma G_{t+1}|S_t=s] \\ &= \mathbb{E}[R_{t}+\gamma V(S_{t+1})|S_t=s] \\ \end{align*} $$
接下来,对于该期望我们可以得到:
$$ \begin{align*} \mathbb{E}[R_{t}+\gamma V(S_{t+1}|S_t=s] &= \mathbb{E}[R_{t}|S_t=s] + \gamma \mathbb{E}[V(S_{t+1})|S_t=s] \\ &= r(s)+ \gamma \sum_{s^{\prime} \in S} P(s^{\prime}|s) V(s^{\prime}) \\ \end{align*} $$
其中,r(s)即时奖励的期望,P(s′|s)是状态s转移到状态s′的概率,即可以用状态转移概率矩阵P来表示。于是上述式子就可以改写为贝尔曼方程(Bellman equation),对每一个状态都成立。
贝尔曼方程
若一个马尔可夫过程有n个状态,即𝒮 = {s1, s2, ⋯, sn},将所有的状态的价值表示为一个列向量V,即:
$$ V = \begin{bmatrix} V(s_1) \\ V(s_2) \\ \vdots \\ V(s_n) \end{bmatrix} $$
同理,将其奖励函数也写为一个列向量R,即:
$$ R = \begin{bmatrix} R(s_1) \\ R(s_2) \\ \vdots \\ R(s_n) \end{bmatrix} $$
于是贝尔曼方程可以表示为:
$$ \begin{align*} V = R + \gamma P V \end{align*} $$
根据矩阵运算可以直接求得一个解析解:
$$ \begin{align*} V &= R + \gamma P V \\ (I - \gamma P)V &= R \\ V &= (I - \gamma P)^{-1} R \\ \end{align*} $$
其中,I是单位矩阵。以上解析解的计算复杂度是O(n3),其中n是状态个数,因此这种方法只适用很小的马尔可夫奖励过程。
马尔可夫决策过程
上述讨论到的马尔可夫过程和马尔可夫奖励过程都是自发改变的随机过程;但如果有一个外界的“刺激”来共同改变这个随机过程,就有了马尔可夫决策过程(Markov decision process,MDP)。我们将这个来自外界的刺激称为智能体(agent)的动作,在马尔可夫奖励过程(MRP)的基础上加入动作,就得到了马尔可夫决策过程(MDP)。马尔可夫决策过程由元组⟨𝒮, 𝒜, P, r, γ⟩构成,其中:
- 状态的集合:𝒮是状态的集合;
- 动作的集合:𝒜是动作的集合;
- 折扣因子:γ是折扣因子;
- 奖励函数:r(s, a)是奖励函数,此时奖励可以同时取决于状态和动作,在奖励函数只取决于状态时,则退化为马尔可夫奖励过程;
- 状态转移函数:P(s′|s, a)是状态转移函数,表示在状态s执行动作a之后到达状态s′的概率。
要理解 马尔可夫奖励过程 (MRP) 和 马尔可夫决策过程 (MDP) 的区别,最本质的核心就在于“谁在掌控”。在LLM训练中,这个区别正好对应 Pre-training 和 RLHF 的区别:
- MRP (类似 Pre-training/Inference):当一个训练好的 LLM 生成文本时,它就像一个 MRP。St: 当前生成的上文。P: 模型固定的概率分布 (Next Token Probability)。如果不加干预,它就是根据概率自己往下“流”,你只能计算这句话生成的“困惑度”或“质量” (Value),但模型参数固定后,过程就是随机游走的。
- MDP (类似 RLHF):当我们引入 PPO 算法进行 RLHF 时,模型变成了 Agent。St: Prompt + 上文。At : 模型决定生成哪个 Token(这个 Token 的选择不再是纯随机,而是为了去拟合 Reward Model 的喜好)。目标: 它可以主动调整策略(Policy π),选择那些能让 Reward Model 给高分的路径。
注意,在上面 MDP 的定义中,我们不再使用类似 MRP定义中的状态转移矩阵方式,而是直接表示成了状态转移函数。这样做一是因为此时状态转移与动作也有关,变成了一个三维数组,而不再是一个矩阵(二维数组);二是因为状态转移函数更具有一般意义,例如,如果状态集合不是有限的,就无法用数组表示,但仍然可以用状态转移函数表示。
策略
在 MDP 中,策略(Policy)定义了智能体在每个状态下应该采取的动作,这个动作的目标是最大化长期累积奖励。策略是一个从状态到动作的映射,即 π : 𝒮 → 𝒜。策略可以用概率分布来表示,即 π(a|s) 表示在状态 s 下采取动作 a 的概率。当一个策略是确定性策略(deterministic policy)时,它在每个状态时只输出一个确定性的动作,即只有该动作的概率为 1,其他动作的概率为 0;当一个策略是随机性策略(stochastic policy)时,它在每个状态时输出的是关于动作的概率分布,然后根据该分布进行采样就可以得到一个动作。
状态价值函数
可以用符号Vπ(s)表示基于策略π下,状态s的价值,定义为从状态出发遵循策略能获得的期望回报,数学表达为:
$$ \begin{align*} V^{\pi}(s) = \mathbb{E}_{\pi}[G_t|S_t=s] \end{align*} $$
其中,Gt是回报,St是状态,π是策略。
动作价值函数
由于动作的存在,可以额外定义一个动作价值函数(action-value function)。用Qπ(s, a)表示在 MDP 遵循策略π时,对当前状态s执行动作a得到的期望回报,数学表达为:
$$ \begin{align*} Q^{\pi}(s,a) = \mathbb{E}_{\pi}[G_t|S_t=s,A_t=a] \end{align*} $$
其中,Gt是回报,St是状态,At是动作,π是策略。
状态价值函数和动作价值函数之间的关系:在使用策略π时,状态s的价值等于在该状态下基于策略采取所有动作的概率与相应的价值相乘再求和的结果:
$$ \begin{align*} V^{\pi}(s) = \sum_{a \in \mathcal{A}} \pi(a|s) Q^{\pi}(s,a) \end{align*} $$
使用策略π时,状态s下采取动作a的价值等于即时奖励加上经过衰减后的所有可能的下一个状态的状态转移概率与相应的价值的乘积:
$$ \begin{align*} Q^{\pi}(s,a) = r(s,a) + \gamma \sum_{s' \in \mathcal{S}} P(s'|s,a) V^{\pi}(s') \end{align*} $$
其中,r(s, a)是奖励函数,P(s′|s, a)是状态转移函数,Vπ(s′)是下一个状态的价值。
贝尔曼期望方程
通过简单推导就可以分别得到两个价值函数的贝尔曼期望方程(Bellman Expectation Equation):
$$ \begin{align*} V^{\pi}(s) &= \mathbb{E}_{\pi}[R_{t} + \gamma V^{\pi}(S_{t+1})|S_t=s] \\ &= \sum_{a \in \mathcal{A}} \pi(a|s) \left( r(s,a) + \gamma \sum_{s' \in \mathcal{S}} P(s'|s,a) V^{\pi}(s') \right) \\ \end{align*} $$
$$ \begin{align*} Q^{\pi}(s,a) &= \mathbb{E}_{\pi}[R_{t} + \gamma Q^{\pi}(S_{t+1},A_{t+1})|S_t=s,A_t=a] \\ &= r(s,a) + \gamma \sum_{s' \in \mathcal{S}} P(s'|s,a) \sum_{a' \in \mathcal{A}} \pi(a'|s') Q^{\pi}(s',a') \end{align*} $$
策略评估
给定一个 MDP ⟨S, A, P, R, γ⟩ 和一个固定的策略 π,我们完全可以将它“降维”成一个 MRP ⟨S, Pπ, Rπ, γ⟩。这一步在强化学习中被称为策略评估(Policy Evaluation)。我
怎么转换?
转换的核心逻辑叫边缘化(Marginalization)。简单来说,既然策略 π(a|s) 已经规定了在每个状态下做动作 a 的概率,那对于环境来说,“动作”这个变量其实就被“平均”掉了。我们只需要把 MDP 中的 P 和 R 按照策略的概率加权平均,就能得到 MRP 的对应项:
A. 转换奖励函数 (Reward),MDP 中,奖励通常取决于“状态”和“动作”:R(s, a)。既然我们知道在状态 s 下,做动作 a 的概率是 π(a|s),那么在这个状态下我们平均能拿到的奖励就是:
$$ \begin{align*} R^\pi(s) = \sum_{a \in A} \pi(a|s) R(s, a) \end{align*} $$
这就变成 了 MRP 中的 R(s),只和状态有关。
B. 转换转移概率 (Transition), 在 MDP 中,转移取决于“状态”和“动作”:P(s′|s, a)。同样的道理,我们在状态 s,下一步去 s′ 的总概率,就是把所有可能动作导致去 s′ 的概率加起来:
$$ \begin{align*} P^\pi(s'|s) = \sum_{a \in A} \pi(a|s) P(s'|s, a) \end{align*} $$
为什么要转换?
这就变成了 MRP 中的 P(s′|s),只和状态有关。在强化学习中需要将MDP 转换为 MRP 的原因有以下三个:
A. 为了“算分” (Policy Evaluation),这是最直接的原因。MDP 的目标是“寻找”最优策略(Planning/Control)。MRP 的目标是“评估”当前状态的价值(Prediction/Evaluation)。当我们想知道“现在的这个策略 π 到底好不好”时,我们需要算出这个策略下的价值函数 Vπ(s)。一旦固定了策略,动作就不再是变量了,整个过程本质上就是一个 MRP。将 MDP 转化为 MRP,让我们能直接套用 MRP 的公式(贝尔曼期望方程)来算出每个状态的分数。
B. 消除非线性 (Removing the max),这是数学求解上的巨大便利。MDP 的贝尔曼最优方程(接下来会介绍)包含一个 max 操作(maxa),这使得方程是非线性的,通常很难直接解,只能通过迭代(如 Value Iteration)逼近。MRP 的贝尔曼方程是线性的(因为动作被平均掉了,没有 max)。
$$ \begin{align*} V = R^\pi + \gamma P^\pi V \end{align*} $$
这本质上就是一个线性方程组 Ax = b 的形式,在状态空间较小时,我们甚至可以直接求逆矩阵 (I − γP)−1 一步到位算出精确解。
C. 视角的切换 (Autopilot),想象在开自动驾驶汽车的场景下:
- MDP (你自己在开):你需要时刻根据路况决定方向盘转多少(选择 a),你关注的是“怎么操作”。
- MRP (开启自动驾驶):系统接管了策略 π。此时对乘客来说,不再需要操心“动作”,车子看起来就是自己在动。你现在只关心“这辆车刚才那个弯过得顺不顺”(评估 V),这就变成了一个 MRP 观测问题。
总结转换方法:对动作 a 进行加权求和(期望)。核心目的:为了评估一个特定的策略好不好。
占用度量
不同策略的价值函数是不一样的。这是因为对于同一个 MDP,不同策略会访问到的状态的概率分布是不同的。首先我们定义 MDP 的初始状态分布为ρ0(s),在有些资料中,初始状态分布会被定义进 MDP 的组成元素中。我们用Ptπ(s)表示采取策略使得智能体在时刻t状态为s的概率,可以得到P0πs = ρ0(s),接下来定义一个策略的状态访问分布(state visitation distribution):
$$ \begin{align*} \rho^{\pi}(s) = (1 - \gamma)\sum_{t=0}^\infty \gamma^t P^{\pi}_t(s) \end{align*} $$
其中,是γ用来使得概率加和为 1 的归一化因子。状态访问分布表示按照当前策略 π 玩下去,在某个时刻出现在状态 s 的概率有多大?注意,理论上在计算该分布时需要交互到无穷步之后,但实际上智能体和 MDP 的交互在一个序列中是有限的。不过我们仍然可以用以上公式来表达状态访问概率的思想,状态访问概率有如下性质:
$$ \begin{align*} \rho^{\pi}(s) =(1-\gamma)\rho_0(s^\prime)+\gamma \int_0^\infty P(s\prime|s,a)\pi(a|s) \rho^{\pi}(s)dsda \end{align*} $$
那么,策略的占用度量就可以定义为:
$$ \begin{align*} \rho^\pi(s, a) &= (1-\gamma)\sum_{t=0}^\infty \gamma^t P^{\pi}_t(s|a)\\ &= \rho^{\pi}(s)\pi(a|s) \end{align*} $$
占用度量表示一个策略下动作状态对被访问到的概率。
两个定理
- 定理 1:智能体分别以策略π和π′和同一个 MDP 交互得到的占用度量ρπ和ρπ′满足:
$$ \begin{align*} \rho^{\pi} = \rho^{\pi'} \Longleftrightarrow \pi= \pi^\prime \end{align*} $$
- 定理 2:给定一合法占用度量,可生成该占用度量ρπ的唯一策略是
$$ \begin{align*} \rho^{\pi} = \frac{\rho^{\pi}(s, a)}{\sum_{a^\prime \in \mathcal{A}} \rho^{\pi}(s, a^\prime)} \end{align*} $$
通常我们定义强化学习的目标是最大化累积回报:
$$ \begin{align*} G(\pi) = \mathbb{E}_{\tau \sim \pi} \left[ \sum_{t=0}^{\infty} \gamma^t R(S_t, A_t) \right] \end{align*} $$
,利用占用度量,我们可以把这个复杂的时序求和公式,重写成一个简单的点积形式:
$$ \begin{align*} G(\pi) = \frac{1}{1-\gamma} \sum_{s \in S} \sum_{a \in A} \rho^\pi(s, a) R(s, a) \end{align*} $$
这个公式揭示了一个事实:我们要找一个最优策略
最优策略
强化学习的目标通常是找到一个策略,使得智能体从初始状态出发能获得最多的期望回报。我们首先定义策略之间的偏序关系:当且仅当对于任意的状态都有 Vπ(s) ≥ Vπ′(s),记π ≥ π′。于是在有限状态和动作集合的 MDP 中,至少存在一个策略比其他所有策略都好或者至少存在一个策略不差于其他所有策略,这个策略就是最优策略(optimal policy)。最优策略可能有很多个,我们都将其表示为π*。最优策略都有相同的状态价值函数,我们称之为最优状态价值函数,表示为:
$$ \begin{align*} V_*(s) = \max_{\pi} V^{\pi}(s) \end{align*} $$
最优策略也有相同的动作价值函数,我们称之为最优动作价值函数,表示为:
$$ \begin{align*} Q_*(s, a) = \max_{\pi} Q^{\pi}(s, a), \forall s \in \mathcal{S}, a \in \mathcal{A} \end{align*} $$
为了使Q*(s, a)最大,我们需要在当前的状态动作对(s, a)之后都执行最优策略。于是我们得到了最优状态价值函数和最优动作价值函数之间的关系:
$$ \begin{align*} Q_*(s, a) = r(s, a) + \gamma \sum_{s' \in \mathcal{S}} P(s'|s, a) V_*(s') \end{align*} $$
这与在普通策略下的状态价值函数和动作价值函数之间的关系是一样的。另一方面,最优状态价值是选择此时使最优动作价值最大的那一个动作时的状态价值:
$$ \begin{align*} V_*(s) = \max_{a} Q_*(s, a) \end{align*} $$
根据Q*(s, a)和V*(s)的关系,我们可以得到贝尔曼最优方程(Bellman optimality equation):
$$ \begin{align*} V_*(s) = \max_{a} Q_*(s, a) \end{align*} $$
$$ \begin{align*} Q_*(s, a) = r(s, a) + \gamma \sum_{s' \in \mathcal{S}} P(s'|s, a) \max_{a'} Q_*(s', a') \end{align*} $$
求解最优策略一般会使用动态规划算法。